[acf field=ver]★[acf field=rate]![acf field=edited]
벡터
학습에 필요한 수준의 이해만 있으면 되기때문에 언급된내용만 잘 이해하는것을 추천하고
심도있는 학습을하면 선형대수학까지 끝도없이 깊어지기때문에 그냥 언급된내용정도만!
벡터
방향과 크기를 동시에 가지고있는 양
일반적인 수학에서는 스칼라 란 크기만으로 계산
전기에서는 방향과 크기를 동시에 가진 벡터란 값을 알아야 계산이가능
(교류에서 계산은 거의 대부분 벡터값계산)
내적과 외적
(1)내적
https://j1w2k3.tistory.com/627
\[ \overline{A}\cdot \overline{B} = |A||B|\cos\theta=A_xB_x +A_yB_y+A_zB_z \]
동일방향
\[i\cdot i=j\cdot j=k\cdot k=1 \]
서로직각
\[i\cdot j=j\cdot k=k\cdot i=0 \]
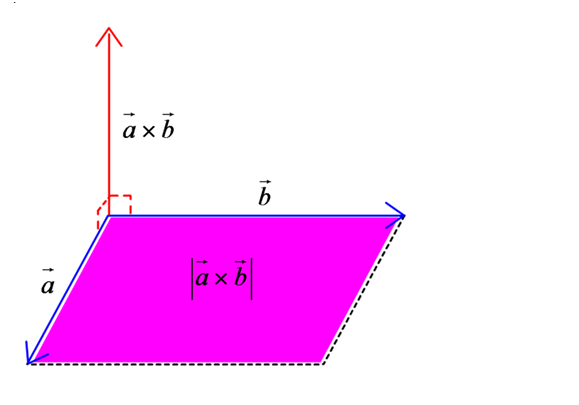
(2)외적
https://j1w2k3.tistory.com/635
\[ \overrightarrow{A}\times \overrightarrow{B}=|\overrightarrow{A}||\overrightarrow{B}|\sin\theta =\begin{vmatrix}i & j & k\\A_x & A_y & A_z\\B_x & B_y & B_z\end{vmatrix} \]
\[ =\begin{vmatrix}A_y & A_z\\B_y & B_z\end{vmatrix}i+
\begin{vmatrix}A_z & A_x\\B_z & B_x\end{vmatrix}j+
\begin{vmatrix}A_x\ A_y\\B_x\ B_y\end{vmatrix}k \]
\[=(A_yB_z-A_zB_y)i+(A_zB_x-A_xB_z)j\]\[+(A_xB_y-A_yB_x)k\]
동일방향
\[i\cdot i=j\cdot j=k\cdot k=0 \]
서로직각(회전성)
\[i\times j=k,\ j\times i=-k,\]
\[\ j\times k=i,\ k\times j=-i,\]
\[ k\times i=j,\ i\times k=-j \]
벡터의 미분
(1)미분연산자 (∇ : Nabla)
\[ \nabla =\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k \]
(2)전위경도 (Gradient 기울기)
증가하고 감소하는 경향
\[ grad V=\nabla V=\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k \]
전계의 세기
전계의 세기는 전위경도와 크기는같고 방향은반대
\[ E=-∇V=-grad V \]
(3)발산 (Divergence)
\[div A= \nabla \cdot A=\frac{\partial A_x}{\partial x} +\frac{\partial A_y}{\partial x}+\frac{\partial A_z}{\partial z}\]
4.회전 (Rotation)(∇ x = rot = curl)
\[ \nabla\times A=rot A =curl A \]
\[ \nabla \times A=\begin{vmatrix}i & j & k\\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\A_x & A_y & A_z\end{vmatrix} \]
\[=(\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z})i+(\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x})j\]\[+(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y})k\]
(5)라플라시안
\[ \nabla^2 =\nabla \cdot\nabla\]\[=\frac{\partial^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}+\frac{\partial^2 }{\partial z^2}=div\ grad \]
푸아송 방정식
전하밀도가 공간적으로 분포하고 있을때 그내부의 임의의 점에서 전위를 결정하는 식
\[ \nabla^2 V=\frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2}=-\frac{\rho}{\epsilon_0} \]
라플라스 방정식
전하분포영역이외의 한점의 전위V를 생각할때는그점에 전하가 없으므로 전위가 0이다
\[ \nabla^2 V = \frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2}=0 \]
(6)가우스의 법칙
\[ div D=∇\cdot D=\rho\]
전하가 존재하는 공간에서는 전속선이 발생한다.
\[ div E=∇\cdot E=\frac{\rho}{\epsilon_0}\]
단위체적에서 발산하는 전기력선의수
=단위체적당 전하량 × 1/ε₀
\[ div E=∇\cdot E=0\]
전하가 존재하지 않는 점은 전기력선의 새로운 발생이나 소멸이 없는 연속을 의미.
좌표계
1.직각좌표법
https://namu.wiki/w/%EC%A2%8C%ED%91%9C%EA%B3%84
\[ \nabla =\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k\]
2.원통좌표법
https://namu.wiki/w/%EC%9B%90%EA%B8%B0%EB%91%A5
\[ \nabla =\frac{\partial }{\partial r}a_r+\frac{\partial }{r\partial \phi}a_{\phi}+\frac{\partial }{\partial z}a_z\]
3.구좌표법
https://namu.wiki/w/%EA%B5%AC(%EB%8F%84%ED%98%95)
\[ \nabla =\frac{\partial }{\partial r}a_r+\frac{\partial }{r \partial \theta }a_\theta+\frac{\partial }{r \sin\theta\partial\phi}a_\phi\]
답글 남기기