[acf field=ver]★[acf field=rate]![acf field=edited]
과도현상/문제RL/문제RC
과도현상
R-L직렬회로
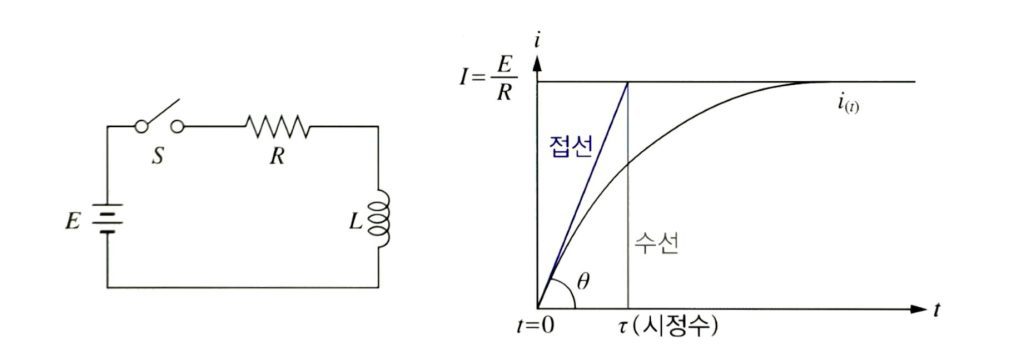
그림의 R-L직렬회로에서 전압인가시 과도현상에 대해 다음 식을 유도하시오
KVL 방정식
\[ Ri(t)+L\frac{d}{dt}i(t)=E \]
전류에 대한 미분방정식으로 정리
\[ L \frac{d}{dt}i(t)+ R i(t)=E \]
미분방정식의 해
1) 과도해
\[ L \frac{d}{dt} i(t) + R i(t) = 0 \]
\[ \to \frac{d}{dt} i(t) + \frac{R}{L} i(t) = 0 \cdot\cdot\cdot (1)식 \]
미분방정식의 일반해
\[i_t(t) =A e ^{st}\ 를\ (1)식에\ 일반해\ 대입\]
\[ \frac{ d} {dt } (A e^{st} )+\frac{ R}{L } (A e ^{st} )=0\]
\[ \to \]
\[A \times s \times e^{st} + A \frac{R}{L} e^{st}\]
\[=A e^{st} (s + \frac{ R}{L }) =0 \]
\[e^{st} \ne 0 이므로 ( s+ \frac{ R} {L} ) =0 \]
\[ ∴ s=-\frac {R} {L}\]
2) 정상해
\[ i_s (t) = \frac{ E}{ R} \]
(t->∞되면, 코일은 단락되어 전류는 저항에 의하여 제한)
1)전류식
\[ i(t)=i_s (t) + i_t (t) = \frac{ E} {R } +A e ^{- \frac{ R} {L }t } \]
\[ \to 초기조건 : i(0)=0[A] \]
조건에서 주어지지 않았지만 0으로 봐도 무관하다.
\[ i(0)=\frac {E}{R} +Ae ^{- \frac{R}{L} 0}=0 \]\[A=-\frac{E}{R}\]
\[ ∴ i(t)= \frac{ E} {R } – \frac{ E}{R } e ^{- \frac{ R}{L }t } = \frac{ E}{ R}(1-e^{- \frac{ R}{L }t} ) [A] \]
라플라스 변환
\[\frac{R}{L}i(t)+\frac{d}{dt}i(t)=\frac{E}{L}\]
\[\frac{R}{L}sI(s)+s^2I(s)=\frac{E}{L}\]
\[I(s)=\frac{\frac{E}{L}}{s(s+\frac{R}{L})}\]
\[ \alpha_1=\lim_{s\to 0}s\frac{\frac{E}{L}}{s(s+\frac{R}{L})}=\frac{E}{R} \]
\[\alpha_2=\lim_{s\to-\frac{R}{L}}(s+\frac{R}{L})\frac{\frac{E}{L}}{s(s+\frac{R}{L})}=-\frac{E}{R}\]
\[I(s)=\frac{E}{R}(\frac{1}{s}+\frac{1}{s+\frac{R}{L}})\]
\[i(t)=\frac{E}{R}(e^0-e^{-\frac{R}{L}t})=\frac{E}{R}(1-e^{-\frac{R}{L}t})\]
2)시정수
t=0인 시점에서 전류의 기울기
\[ \tan\theta=\frac{d}{dt}i(t)|_{t=0}\]
\[=\frac{d}{dt} (\frac{E}{R} (1-e^{-\frac{R}{L}t}) )|_{t=0}\]
\[=-\frac{E}{R}\times(-\frac{R}{L})\times e^ {- \frac{ R} { L}0}\]
\[=\frac{E}{L} =\frac{\frac{E}{R}}{\tau} \]
\[∴ \tau=\frac{L}{R}[sec]\]
… 충전시 63.2%에 도달하는 시간
… 방전시에는 36.8%에 도달하는 시간
3)전압식
- 저항에 걸리는 전압
\[ E_R=Ri(t)=R\frac{E}{R}(1-e^{-\frac{R}{L}t}))|_{t=0} \]
\[=E(1-e^{-\frac{R}{L}t})[V]\]
- 인덕턴스에 걸리는 전압
\[ E_L=L\frac{dt(t)}{dt}=L\frac{d}{dt}(\frac{E}{R}(1-e^{-\frac{R}{L}t}))\]\[=Ee^{-\frac{R}{L}t}[V]\]
4)전력량식
\[ W_R=\int_0^t E_R(t)i(t)dt \]
\[=\int_0^t E(1-e^{-\frac{R}{L}t})\frac{E}{R}(1-e^{-\frac{R}{L}t})dt\]
\[=\frac{E^2}{R}t+\frac{E^2 L}{R^2}(2e^{-\frac{R}{L}t}-\frac{1}{2}e^{-\frac{2R}{L}t}-\frac{3}{2})\]
\[ W_L=\int_0^t E_L(t)i(t)dt\]
\[=\int_0^t Ee^{-\frac{R}{L}t}\frac{E}{R}(1-e^{-\frac{R}{L}t})dt\]
\[=\frac{E^2L}{R^2}(e^{-\frac{R}{L}t}+\frac{1}{2}e^{-\frac{2R}{L}t}+\frac{1}{2})\]
\[ W=\int_0^t E(t)i(t)dt\]
\[=\int_0^t E\frac{E}{R}(1-e^{-\frac{R}{L}t})dt\]
\[=\frac{E^2}{R}t+\frac{E^2L}{R^2}(e^{-\frac{R}{L}t}-1)\]
- 인덕턴스에 저장되는 에너지
\[W_L=\int^∞_0E_L(t)i(t)dt\]
\[=\int^∞_0Ee^{-\frac{R}{L}t}\frac{E}{R}(1-e^{-\frac{R}{L}t})dt\]
\[=[\frac{E^2L}{R^2}(-e^{-\frac{R}{L}t}-\frac{1}{2}e^{-\frac{R}{L}t}+\frac{1}{2})]^∞_0\]
\[=\frac{1}{2}LI^2[J]\]
R-C직렬회로
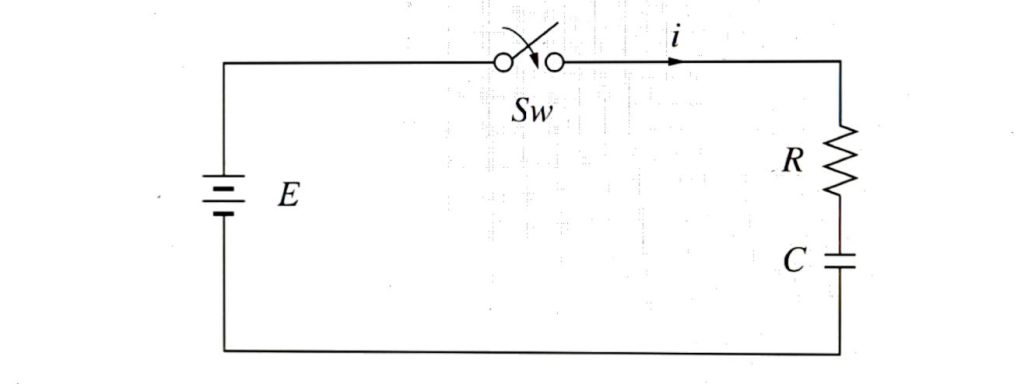
위의 그림과 같은 R-C직렬회로에서 t=0인 순간에 스위치를 닫는 경우 흐르는 전류(i), 시전수(τ), 저항에 걸리는 전압(V), 콘덴서에 충전되는 전압(V)을 구하시오. 단, 콘덴서에 초기전압은 없다.
1.KVL방정식
\[ R i(t) +v (t) =E \]
2. 전압에 대한 미분방정식으로 정리
\[ RC\frac{dv(t)} {dt} +v(t)=E … 충전 \]
3. 미분방정식의 해
1) 과도해
\[ RC \frac{dv(t)} {dt} +v(t)=0 \]\[\to \frac{dv(t)}{dt} + \frac{1}{RC} v(t)=0 … (1)식 \]
\[ 미분 방정식의 일반해 v_t (t) =A e^{st} 를 (1)식에 대입
\]
\[ \frac{ d (Ae^{st} )} { dt} + \frac{ 1}{RC } (Ae^{st} ) = 0 \]
\[\to A \times s \times e^{st} + \frac{ A}{RC } \times e^{st} =0 \]
\[ A e^{st} ( s + \frac{ 1}{RC }) =0 , e^{st} \ne 0 이므로 ( s+ \frac{ 1}{ RC}) =0 \]
\[ s=-\frac{ 1}{RC } \]
2) 정상해
\[ v_s (t) = E \]
( t->∞ 되면, 커패시터는 개방되어 모든 전압이 커패시터에 분압된다)
1)전류식
- 라플라스 변환
\[ Ri(t)+\frac{1}{C}\int_0^t i(t)dt=E \]
\[i(t)+\frac{1}{RC}\int_0^t i(t)dt=\frac{E}{R}\]
\[sI(s)+\frac{1}{RC}I(s)=\frac{E}{R}\]
\[I(s)=\frac{\frac{E}{R}}{(s+\frac{1}{RC})}\]
\[i(t)=\frac{E}{R}e^{-\frac{1}{RC}t}\]
2)시정수
\[ \tan\theta=\frac{di(t)}{dt}|_{t=0}\]
\[=\frac{d}{dt}\frac{E}{R}e^{-\frac{1}{RC}t} |_{t=0}\]
\[=\frac{E}{R}(-\frac{1}{RC})=-\frac{E}{R^2C}\]
\[ \tan\theta=\tau=RC \]
3)전압식
- 저항에 걸리는 전압
\[ E_R=Ri(t)=R\frac{E}{R}e^{-\frac{1}{RC}t}=Ee^{-\frac{1}{RC}t}[V] \]
- 콘덴서에 충전되는 전압
\[ E_C=\frac{1}{C}\int_0^ti(t)dt \]
\[= \frac{1}{C}\int_0^t\frac{E}{R}e^{-\frac{1}{RC}t}dt\]
\[=E(1-e^{-\frac{1}{RC}t})[V]\]
4)전력량식
\[ W_R=\int_0^t E_R(t)i(t)dt \]
\[=\int_0^tEe^{-\frac{1}{RC}t}\frac{E}{R}e^{-\frac{1}{RC}t}dt\]
\[=\frac{1}{2}CE^2(1-e^{-\frac{2}{RC}t})\]
\[W_C=\int_0^t E_C(t)i(t)dt\]
\[=\int_0^tE(1-e^{-\frac{1}{RC}t})\frac{E}{R}e^{-\frac{1}{RC}t}dt\]
\[=E^2C(-e^{-\frac{1}{RC}t}+\frac{1}{2}e^{-\frac{2}{RC}t}+\frac{1}{2})\]
\[ W=\int_0^tE(t)i(t)\]\[=\int_0^tE\frac{E}{R}e^{-\frac{1}{RC}t}dt\]
\[=E^2C(1-e^{-\frac{1}{RC}t})\]
- 콘덴서에 저장되는 에너지
\[ W_C=\int_0^∞E_C(t)i(t)dt \]
\[=\int_0^∞E(1-e^{-\frac{1}{RC}t})\frac{E}{R}e^{-\frac{1}{RC}t}dt\]
\[=E^2C[-e^{-\frac{1}{RC}t}+\frac{1}{2}e^{-\frac{2}{RC}t}+\frac{1}{2}]_0^∞\]
\[=\frac{1}{2}CE^2\]
답글 남기기