[acf field=ver]★[acf field=rate]![acf field=edited]
회로망의 재정리
회로 해석법⁕
테브난과 노튼의 정리/회로 해석법 문제1/회로 해석법 문제2
테브난의 정리
(Thevenin’s Theorem)
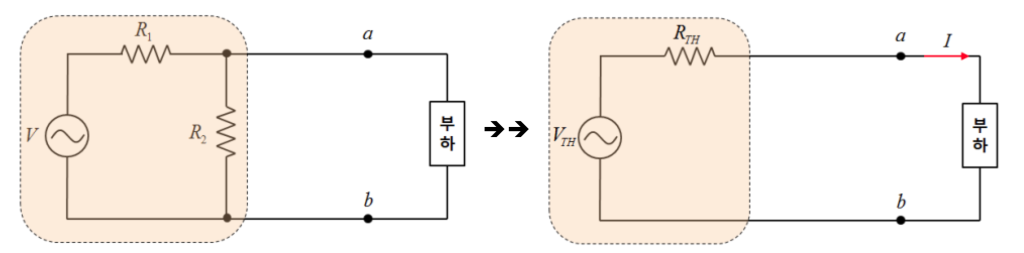
- 능동회로부를 하나의 전압원(Vth)과 하나의 임피던스(Zth)가 직렬로 연결된것으로 등가화한 이론
- 선형회로에서 두개의 단자를 지닌 전압원, 전류원, 저항의 어떠한 조합이라도 하나의 전압원 V와 하나의 직력저항 R로 변화하여 전기적 등가를 설명하기위한회로
- AC시스템에서 테브난의 정리는 단순한 저항이 아닌, 일반적인 임피던스로 적용할수 있다.
- 고장전류를 계산하는 데 사용된다.
\[I=\frac{V_{2}}{R_{2}+R_{1}}\]
노튼의 정리
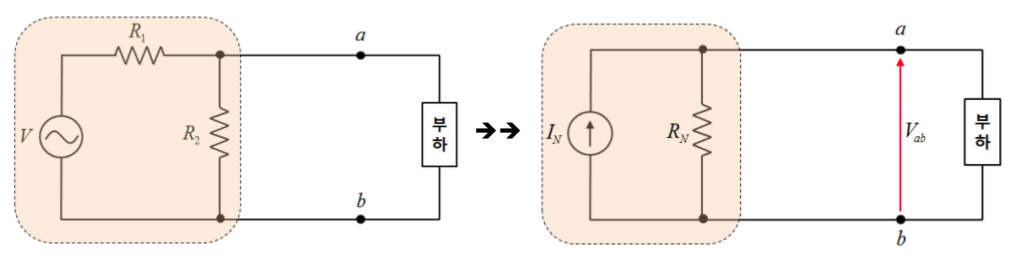
- 능동 회로부를 하나의 전류원(IN)과 하나의 임피던스(RN)가 병렬로 연결된 것으로 등가화 이론
- 선형 전기회로에서 두 개의 단자를 지닌 전압원, 전류원, 저항의 어떠한 조합이라도 이상적인 전류원 I와 병렬저항 R로 변환하여 전기적 등가를 설명하기위한 정리이다.
- AC시스템에서 노튼의 정리는 단순히 저항이 아닌 일반적인 임피던스를 적용할수있다.
1)In :
a, b 두단자를 단락했을때의 a, b단자에 흐르는 전류(단락전류)
\[I_N=\frac{V}{R_1}\]
2)Rn :
능동회로의 전원을 모두 제거하고 A, B단자에서 전원측을 바라본 임피던스(전압 : 단락처리, 전류원 : 개방처리)
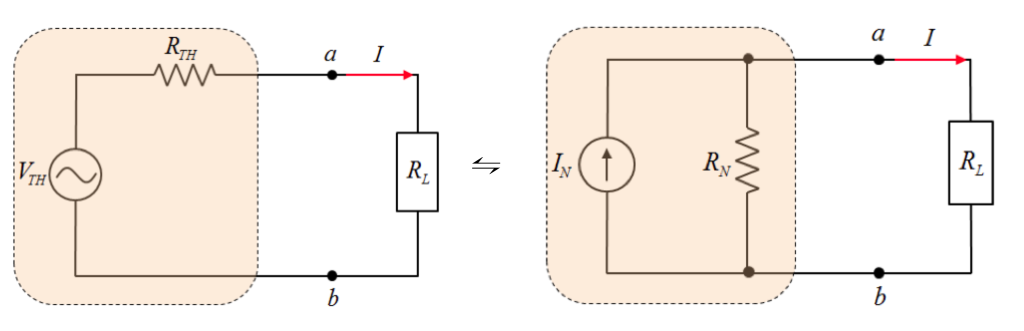
\[R_N=R_{TH}=\frac{R_1×R_2}{R_1+R_2}\]
3)부하에 흐르는 전류
\[ I = \frac{ V_{TH}} { R_{TH} + R_L} \cdot\cdot\cdot테브난 정리\]
\[ I = \frac{ R_N \times I_N} { R_N + R_L}=\frac{ R_N \times \frac{ V_{TH}} {R_N} } {R_N +R_L }\]\[=\frac{ V_{TH}} {R_N +R_L } \cdot\cdot\cdot노튼정리\]
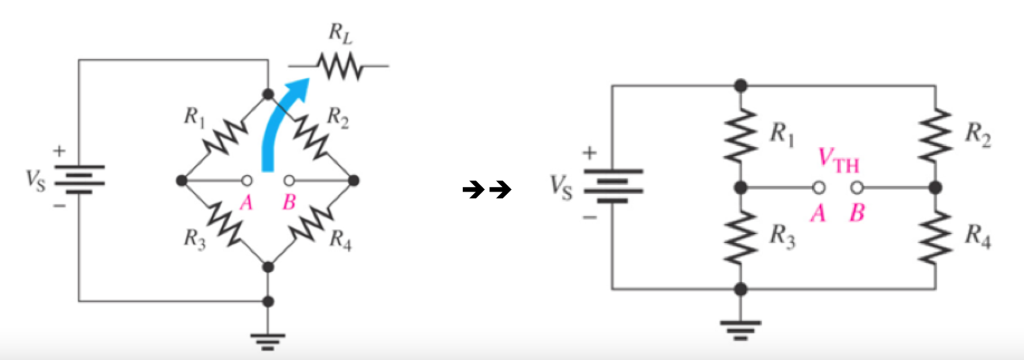
\[ V_A=\frac{ R_3 } {R_1 + R_3 } \times V_s \]
\[ V_B =\frac{ R_4 } {R_2 + R_4 } \times V_s \]
\[\to \to\]\[ V_{TH} =V_A -V_B \]
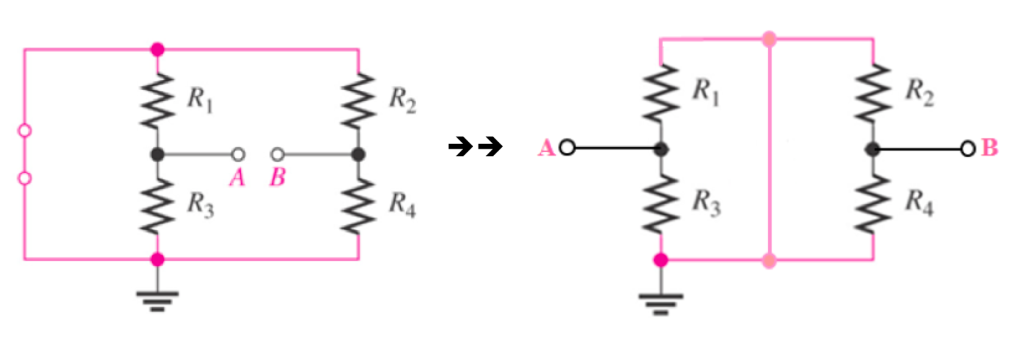
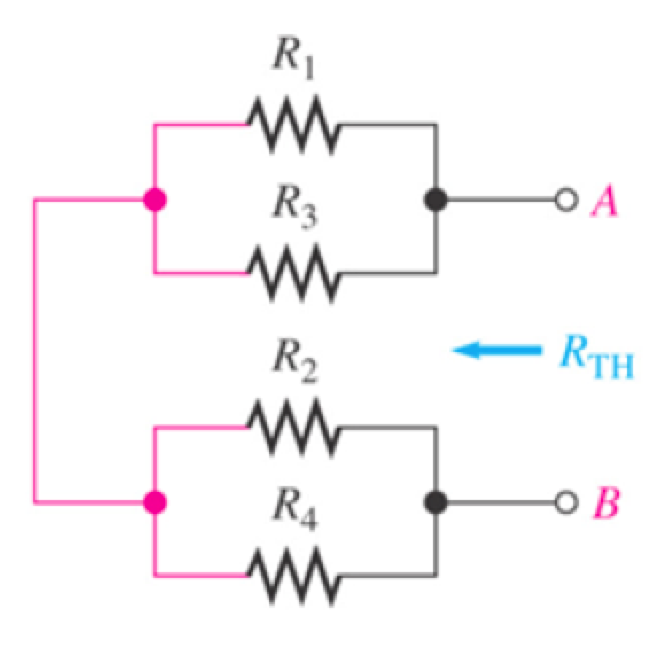
\[ R_{TH} =\frac{ R_1 \times R_3}{ R_1 + R_3} + \frac{ R_2 \times R_4 } {R_2 +R_4 } \]
밀만의 정리/밀만의 정리 문제1/밀만의 정리 문제2/밀만의 정리 문제3/밀만의 정리 문제4/밀만의 정리 문제5
밀만의 정리
(Millman’s theorem)
- 주파수가 동일한 전원이 회로망 내에 병렬로 연결되어 있을때 임의의 2단자간의 전압을 구하는데 유용한 정리
- 전류는 각각 전원을 내부임피던스로 단락시켰을 때 단락전류의 값이다.
- 선형 전기회로에서 내부저항을 갖는 전압원이 병렬접속될 경우 양 단자에 나타내는 전압을 평리하게 구하는 방법을 제공하는 정리이다
- AC시스템에서 밀만의 정리는 단순히 저항이 아닌, 일반적인 임피던스를 적용할 수 있다
1)a,b사이에 나타나는 전압
\[ V_{ab}=(\frac{E_1}{R_1}+\frac{E_2}{R_2}+\frac{E_3}{R_3}) \times \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}} \]
\[=\frac{\frac{E_1}{R_1}+\frac{E_2}{R_2}+\frac{E_3}{R_3}} {\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}} [V] \]
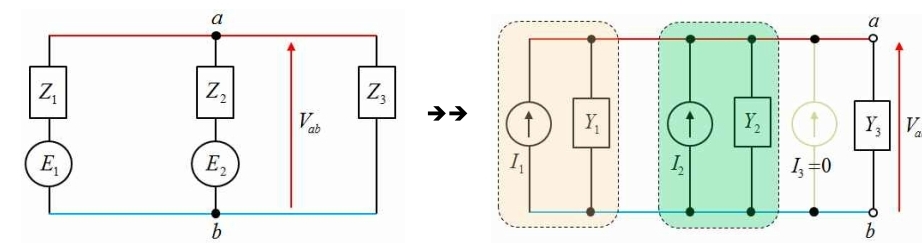
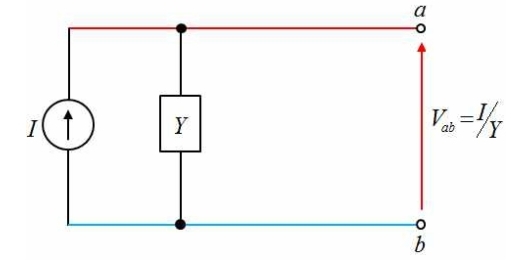
\[ I_1=\frac{E_1}{Z_1}, I_2=\frac{E_2}{Z_2}, I_3=\frac{0}{Z_3}=0\]\[ \to I=I_1+I_2+0…합성단락전류 \]
\[Y_1=\frac{1}{Z_1}, Y_2=\frac{1}{Z_2},Y_3=\frac{1}{Z_3}\]\[ \to Y=Y_1+Y_2+Y_3…합성어드미턴스 \]
중첩의원리/중첩의원리 문제1/중첩의원리 문제2
중첩의 원리
(Principle of Superposition)
- 선형 전기회로에서 다수의 독립전원이 있는 경우 주어진 소자의 전압이나 전류값을 구할 경우 독립전원을 개별적으로 구하여 합하는 방식을 중첩의 원리라 한다.
1)회로망 내에 서로 다른 전원이 있는 경우에 서로의 전원을 독립적으로 해석하여 각각의 해석 값을 중첩하여 더해준다.
2) 해석조건 : 전압원 단락 전류원 개방처리

답글 남기기