0.6.0★N!220709
수동소자(R,L,C)의 페이저 해석
허수의 단위 j의 의미
\[ j=1\angle 90° \]
\[ j^2=(1\angle 90° )^2\]
\[ j^3=(1\angle 90°)^3\]
\[j^4=(1\angle90°)^4\]
수동소자(R, L, C)의 페이저해석
\[ Z_R=R\ [\Omega] \]
\[ Z_L=j\omega L =\omega L\angle 90° [\Omega]\]
\[ Z_C=\frac{1}{j\omega C}=-j\frac{1}{\omega C}=\frac{1}{\omega C}\angle -90° \ [\Omega] \]
전류전압의 위상(Phase)
1)위상
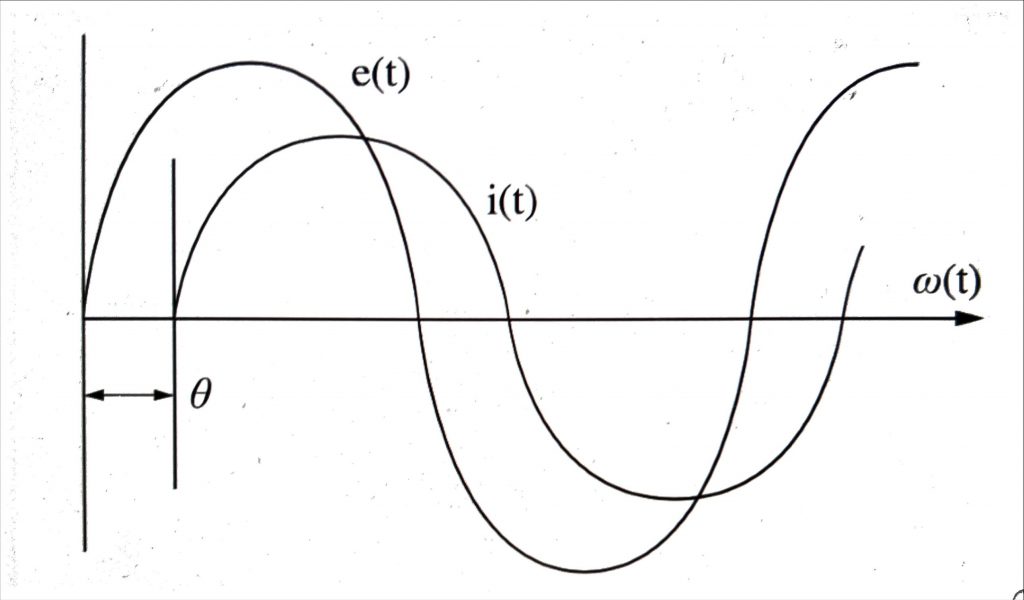
- 교류의 경우 e=Em sin(wt+θ)에서 wt+θ를 위상이라 한다. 주파수가 일정한 교류회로에서는 일반적으로 θ만이 문제가 되므로 θ만 위상이라고도 한다
- 다음 그림과 같이 전압 e=Em sin(wt) 와 전류 i=Im sin(wt+θ)의 위상차는 wt-(wt-θ)=θ 가 된다.
- 전압과 전류의 위상차에 의해 역률이 발생한다
- 진상역률 : 일반 전력계통에서 전류가 전압보다 위상이 뒤진다
- 진상역률 : 유전체에서 전류가 전압보다 위상이 앞선다
2)전류가 전압보다 위상이 뒤지는 이유
(지상역률의 원인)
- 이상적인 리액터를 가정하면, 다음 두가지 방법으로 증명할수 있다
- 그러므로 전류가 전압보다 90 위상이 뒤진다.
\[e=L\frac{di}{dt}\]
\[\int edt=Li \]
\[ i=\frac{1}{L}\int edt =\frac{1}{L} \int E_m \sin \omega tdt \] \[ =-\frac{E_m}{\omega L}\cos\omega t\]
\[=\frac{E_m}{\omega L }\sin(\omega t -\angle 90 )\]\[=\frac{E_m}{\omega L}\sin\omega t\angle -90=\frac{e}{j\omega L}\]
\[ e=L\frac{di}{dt}\] \[=L\frac{d}{dt}I_m\sin\omega tdt\]
\[=\omega LI_m\cos\omega t\] \[ \omega LI_m\sin(\omega t+90)\]\[\omega LI_m\sin\omega t\angle90\]\[=j\omega Li\]
3)전류가 전압보다 위성이 앞서는 이유
(진상역률의 원인)
\[ e=\frac{1}{C}\int I_m \sin \omega t dt \]\[=-\frac{I_m}{\omega C}\cos \omega t \]\[ =\frac{I_m}{\omega C}\sin(\omega t-90)\]\[=\frac{I_m}{\omega C}\sin\omega t\angle-90=\frac{I_m}{j\omega C}\]
- 그러므로 전류가 전압보다 90 위상이 앞선다
답글 남기기