비정현파 교류
파형
- 파형률과 파고율
일반적으로 비정현파는 정현파 외에 여라 가지 파형이 중첩되어 있는데
이를 실효값으로 표현하면 파형의 특성을 알 수 없어 파형률과 파고율로 표현한다
\[파고율=\frac{파고값}{실효값}\]
- 파고율 : 비정현파의 파형의 평활도로 나타냄
\[ 파형율=\frac{실효값}{평균값}\]
- 파형율 : 파형의 날카로운 정도를 나타냄
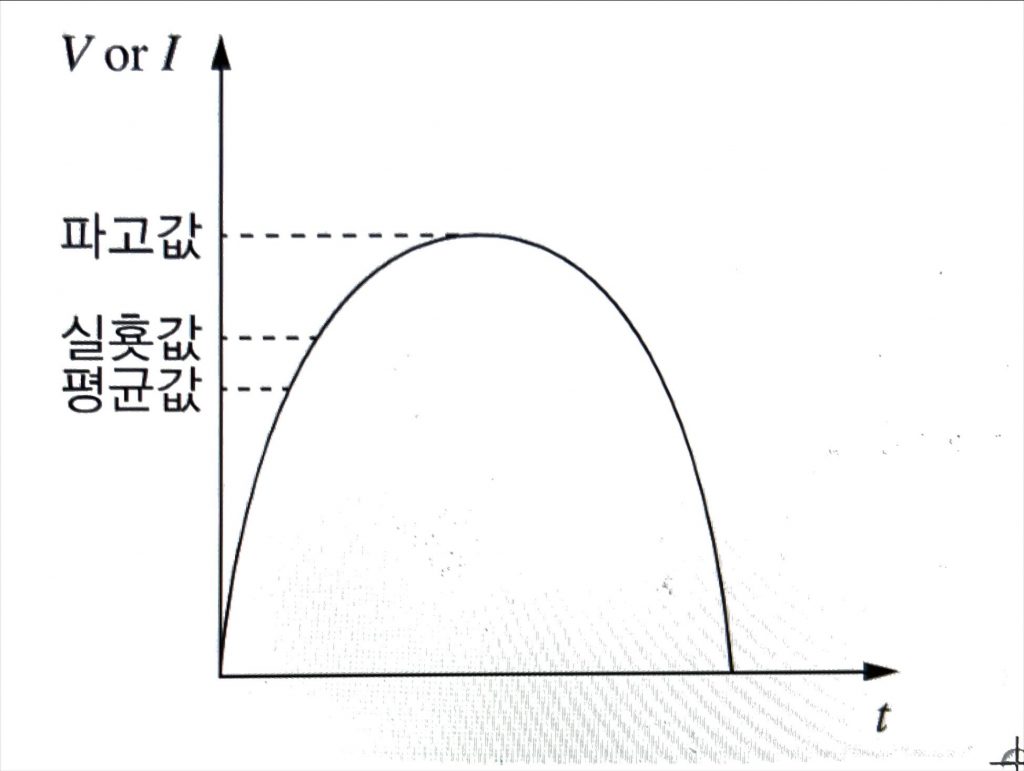
- 정현파의 파형률, 파고율
\[ I_m이면 그 실효값은 I=\frac{I_m}{\sqrt{2}}\]\[평균값은 I_{av}=\frac{2}{\pi}I_m이므로\]
\[파형율=\frac{\frac{1}{\sqrt{2}}I_m}{\frac{2}{\pi}I_m}=\frac{\pi}{2\sqrt{2}}\sim1.11 \]
\[파고율=\frac{I_m}{\frac{1}{\sqrt{2}}I_m}=\sqrt{2}=1.414\]
- 기타 파형의 파형률, 파고율
| 명칭 | 파형 | 파형율 | 파고율 |
|---|---|---|---|
| 방형파 | 1.0 | 1.0 | |
| 반원파 | 1.04 | 1.226 | |
| 방물선파 | 1.10 | 1.370 | |
| 정현파 | 1.11 | 1.414 | |
| 삼각파 | 1.155 | 1.732 |
왜형율
(THD : Total Harmonics Distortion)
- 고조파(Harmonics)
기본 주파수에 대해 2배 3배 4배와 같이 정수 배에 해당하는 물리적 전기량 - 종합 고조파 왜형율(THD : Total Harmonics Distortion)
기본파 성분에 포함된 고조파 성분의 비율
\[ I_{THD}=\frac{\sqrt{\sum _{h=2}^nI_h^2}}{I_1} \]
\[ V_{THD}=\frac{\sqrt{\sum _{h=2}^nV_h^2}}{V_1} \]
여기서, V1,I1 : 기본파의 전압 또는 전류의 실효값
Vh,Ih: h차 고조파의 전압 또는 전류의 실효값
- 전류 총수요 왜형율(TDD : Total Demand Distortion)
- 고조파 전류와 최대 부하전류의 비
\[ I_{TDD}=\frac{\sqrt{\sum _{n=2}^{∞}}I_h^2}{I_L}\times100 \]
- 수용가 고조파 문제는 TDD가 중요해진다
푸리에 급수
- 개요
푸리에 급수란 모든 주가함수는 사인 코사인의 합으로 나타낼수 있다는 것이다. 즉, 다음과 같은 함수로 나타낼 수 있다
\[ f(x)=a_0+\sum_{n=1}^{∞}(a_n \cos nx+b_n\sin nx) \]
\[ f(x)=\frac{1}{\pi}\int_{-n}^\pi f(x)dx \]\[+\sum_{n=1}^∞ [(\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx)\cos nx \]\[ +(\frac{1}{\pi}\int_{-\pi}^{\pi}f(x) \sin nxdx)\sin x]\]
- 푸리에 급수의 적용
푸리에 급수는 비정형파를 다루는 데 유용한 해석방법이다
답글 남기기