[acf field=ver]★[acf field=rate]![acf field=edited]
도심지 대형 건축물의
구조체 접지설계 시 검토사항
접지 형태(접지전극)의 분류
1)인공접지
- 봉형 접지전극의 병렬 배치
- 망상 접지전극 등 다른 종류의 접지전극을 조합하여 사용
2)자연접지
- 건출물 구조체 및 금속제 수도관 등을 이용하여 대지에 매설된 도전성 물체를 접지전극으로 대용한 것
건축물 구조체 접지방식
1)정의
- 별도의 접지전극을 설치하지 않고 건출물 구조체의 일부인 철골, 철근을 접지전극으로 이용하는 설비이다
2)조건
- 구조체는 반드시 도전성일 것
- 요구되는 접지저항값 이하일 것
3)종류
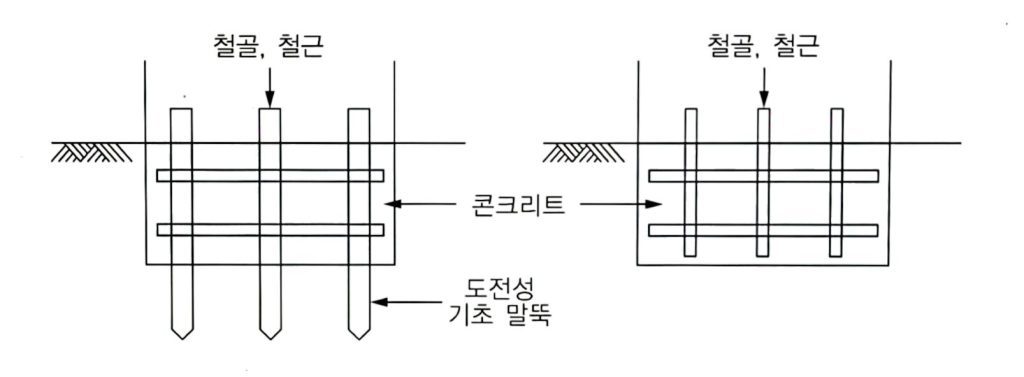
- 철골, 도전성 기초 말뚝이 대지에 매입된 경우
- 철골, 철근이 콘크리트에 매입된 경우
4)콘크리트 전기저항률 영향인자.
- 시멘트, 모래 자갈의 배합니
- 흡수율
- 수질
- 주위환경
- 온도, 습도, 계절적 변동
5)건축물 구조체 전기적 특성
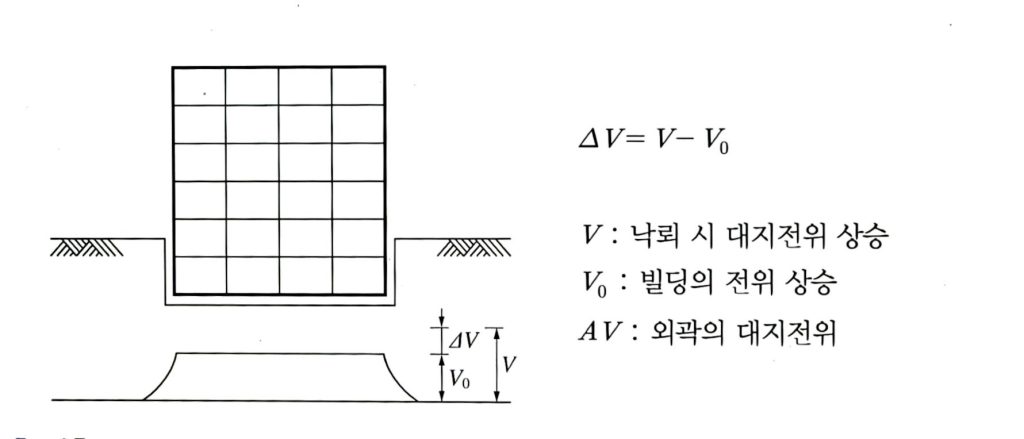
- 낙뢰가 건축물의 구조체에 입사한 경우 : 뇌격전류는 구조체를 통하여 대지로 흐른다
- 구조체의 접지저항이 작으면 전위 상승도 낮아져 전위 상승의 파급이 없다
- 구조체 접지는 인공 접지에 비해 접지저항값이 대단히 낮다
- 대지와의 접촉면적이 넓으므로 접지 임피던스도 낮은 고주파 영역에서도 양호한 전기적 특성을 가진다
- 도심지나 산간지역의 면적이 제한되어 있는 장소에서는 구조체 접지전극 활용이 바람직하다
6)건축물 구조체 접지저항 계산방법
- 등가표면적 치환법
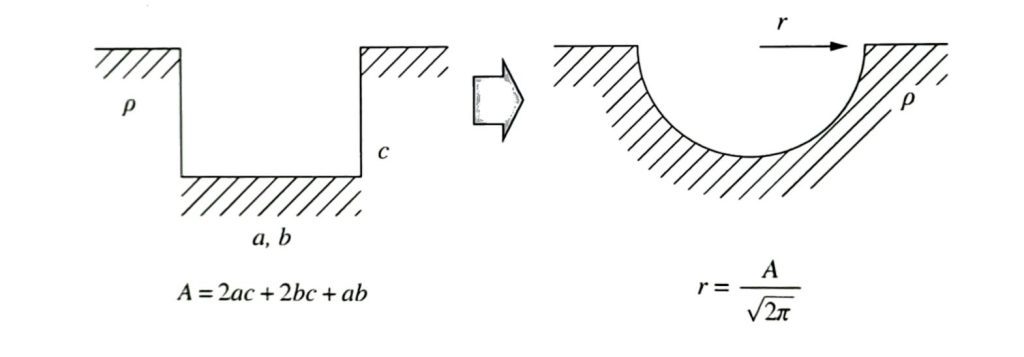
\[R=\frac{\rho}{2\pi r}=\frac{\rho}{\sqrt{2\pi A}}[\Omega]\]
- 등가 체적 치환법
건축물의 지하구조를 반구형 접지극으로 간주하여 구하는 방식
반구의 체적은
\[V=\frac{2}{3}\pi r^3[m^3]\]
\[r=\sqrt[3]\frac{3V}{2\pi}=0.7816\times\sqrt[3]V[m]\]
\[R=\frac{\rho}{2\pi r}=\frac{\rho}{2\pi\times 0.7816\times\sqrt[3]V}\]\[=0.2\times\frac{\rho}{\sqrt[3]V}[\Omega]\]
\[V=(0.2\times\frac{\rho}{R})^3[㎥]\]
- 형상계수법
건축물의 지하구조의 형상계수를 이용하는 방법
건축물 지하구조의 저항은
\[R=\frac{K\times\rho}{L}[\Omega]\]
L:지하구조의 가로, 세로, 깊이 중 가장 긴 변[m]
K:형상계수로서 깊이와 세로 비,
가로와 세로 비 등에 따라 결정되는 값
(0.15~0.45정도의 값)
- 결론
- 콘크리트에 매입된 기초접지극을 통한 접지저항 계산 시 간편한 계산법인 등가체적법을 주로 사용
- 등가치환법에 의한 접지저항의 계산이 다른 계산방법에 비하여 다소 낮게 계산되므로 이를 고려해야 한다
건축물 구조체 문제점
- 대규모 구조체의 접지저항 측정이 곤란
- 도심지에서 접지저항 실측이 불가능
- 기초공사 전 접지공사로 공사 완료 후 저항값 측정 곤란
- 대규모 접지저항 측정은 전위강하법 채용
- 저항값이 작아 외부 영향을 받기 쉬우며 오차 발생 확률이 높다
- 이론적 추정값과 접지저항 추정값이 상당한 차이 발생
★ 접지방법결정 (EM)
(목적에따른)
N 중성점 접지방법
R 유효접지와 비유효접지
B 배전계통의 접지(IEC 60364-3 )
(형태에따른)
O 단독접지와 공용접지
S 구조체 접지설계 시 검토사항
T 통합 공통접지방식
E 등전위 본딩
G 접지선 접지봉
T 접촉전압과 보폭전압

답글 남기기