[acf field=ver]★[acf field=rate]![acf field=edited]
61.8%법칙
전위강하법으로 측정할 경우 보조 접지전극 P는 간격 사이의 61.8% 지점에 설치하여야 정확한 측정이 가능
전위강하법 구성
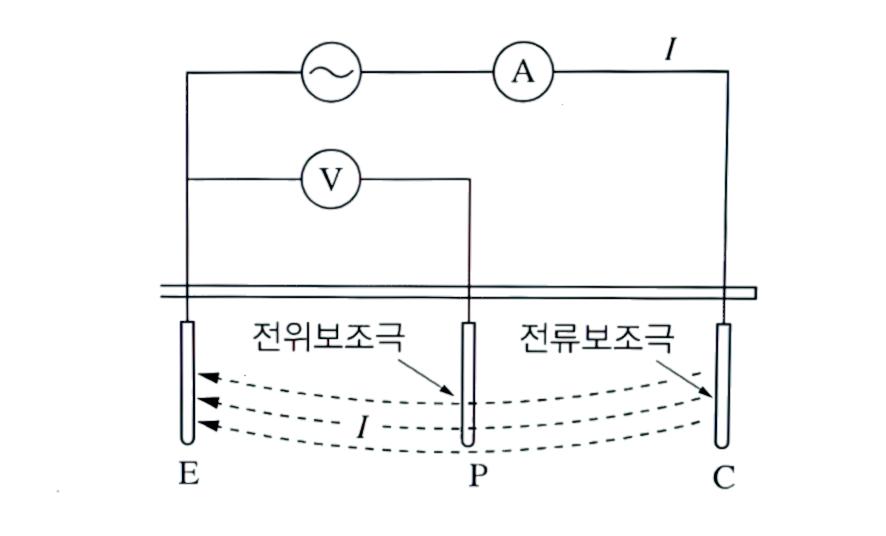
수식적 증명
1)E 전극에서 전류 I가 유입하는 경우 전위차
\[V_1=E와 P 전압(E기준에서 전압)\]
\[V_1=\frac{\rho I}{2\pi r}-\frac{\rho I}{2\pi P}\]
2)C 전극에서 전류 I가 유출하는 경우 전위차
\[V_2=E와 P 전압(E기준에서 전압)\]
\[V_2=\frac{\rho I}{2\pi C}-(-\frac{\rho I}{2\pi (C-P)})\]
3)E, P전극 간의 전위
\[V=V_1+V_2=\]
\[(\frac{\rho I}{2\pi r}-\frac{\rho I}{2\pi P})+[-\frac{\rho I}{2\pi C}-(-\frac{\rho I}{2\pi(C-P)})]\]
4)접지저항
\[V=\frac{\rho I}{2\pi r}\]
이면 측정값이 참값과 같다.
∴반구형의 접지저항은
\[R=\frac{\rho}{2\pi r}\]
이므로, 상기식으로부터
\[-\frac{\rho I}{2\pi P}-\frac{\rho I}{2\pi C}-\frac{\rho I}{2\pi (P-C)}=0\]
이어햐 한다.
\[-\frac{1}{P}-\frac{1}{C}-\frac{1}{(P-C)}=0\]
\[\frac{P^2+CP-C^2}{PC(P-C)}=0\]
근의 공식을 적용하면
\[P=\frac{-C±\sqrt{C^2+4C^2}}{2}=0.618 C\]
★접지 설계 (EP)
E 접지
O 접지설계
N 토양특성 검토
R 대지구조 해석방법
D 접지저항 저감
B 보링공법(수직공법)
P PGS공법
C 접지저항측정법
6 61.8%법칙
KEC140

답글 남기기